MLOps Blog

Lossless Data Compression Using Arithmetic Encoding in Python and Its Applications in Deep Learning

Ahmed Gad

11 min

25th August, 2023

ML Model Development

Data compression algorithms represent a long sequence of symbols using a fewer number of bits than the original representation. There are 2 categories of data compression algorithms: lossy and lossless.

In this tutorial, we’ll discuss a lossless algorithm called arithmetic encoding (AE). You’ll see how AE works through an example that shows the steps of encoding and decoding a message.

We’ll also build a Python implementation that can encode and decode text messages. The implementation is available at this GitHub project.

Here’s everything that we’ll cover in this tutorial:

Overview of Arithmetic Encoding
Frequency & Probability Tables
Encoding
Decoding
decimal Module
Python Implementation
Applications of Lossless Compression in Deep Learning

Let’s start!

Overview of the lossless algorithm (Arithmetic Encoding)

In data compression, lossy algorithms compress data while losing some details. They reduce the number of bits used to represent the message, even if that reduces the quality of reconstructed data.

Lossless algorithms reconstruct original data without any loss. Because of this, they use a higher number of bits compared to lossy algorithms.

Arithmetic encoding (AE) is a lossless algorithm that uses a low number of bits to compress data.

It’s an entropy-based algorithm, first proposed in a paper from 1987 (Witten, Ian H., Radford M. Neal, and John G. Cleary. “Arithmetic coding for data compression.” Communications of the ACM 30.6 (1987): 520-540).

One reason why AE algorithms reduce the number of bits is that AE encodes the entire message using a single number between 0.0 and 1.0. Each symbol in the message takes a sub-interval in the 0-1 interval, corresponding to its probability.

To calculate the probability of each symbol, a frequency table should be given as an input to the algorithm. This table maps each character to its frequency.

The more frequent the symbol, the lower number of bits it is assigned. As a result, the total number of bits representing the entire message is reduced. This is compared to using a fixed number of bits for all symbols in the message as in Huffman coding.

Frequency table

To encode (= compress) a message using AE, you need these inputs:

The message you want to encode.
The frequency table of all possible symbols in the message.

The frequency table is usually calculated by analyzing different messages and concluding by the number of times each symbol is repeated.

For example: assume that the messages to be encoded consist of just 3 symbols a, b, and c. By analyzing some previous messages (e.g. babb, cbab, and bb), we get the frequencies of the 3 symbols:

Based on the frequency table, how do you encode a message like abc using AE? Before you start encoding, you need to calculate a probability table out of the frequency table.

Probability table

Using the frequency table, we can calculate the probability of occurrence of each symbol. The probability is calculated as follows:

Frequency of a symbol/Sum of frequencies of all symbols

Based on the frequency table, here are the probabilities of our 3 symbols:

p(a)=2/10=0.2
p(b)=7/10=0.7
p(c)=1/10=0.1

Given the message and the probability table, AE can start the encoding process.

Encoding

Encoding in AE works by representing the cumulative probabilities of all symbols on a line that ranges from 0.0 to 1.0. On that line, each symbol uses a sub-range.

Given any symbol C, it starts from the value Sand ends at the value calculated using the following equation:

S+(P(C))*R

Where:

S: The cumulative sum of all previous probabilities.
P(C): The probability of symbol C.
R: The range of line which is calculated by subtracting the start from the end of the line.

In the beginning, the line starts from 0.0 and ends at 1.0, thus R=1.0.

Let’s calculate the start and end values of the 3 symbols a, b, and c.

For the first symbol, a, it starts from 0.0 to 0.0+(0.2)*1.0=0.2. The start value is 0.0 because it’s the first symbol. The range is (0.0:0.2).
For the second symbol, b, it starts from 0.2 to 0.2+(0.7)*1.0=0.9. The range is (0.2:0.9).
The third symbol, c, starts from 0.9 to 0.9+(0.1)*1.0=1.0. The range is (0.9:1.0).

Given the ranges of all symbols, it’s good to represent them graphically, as in this figure:

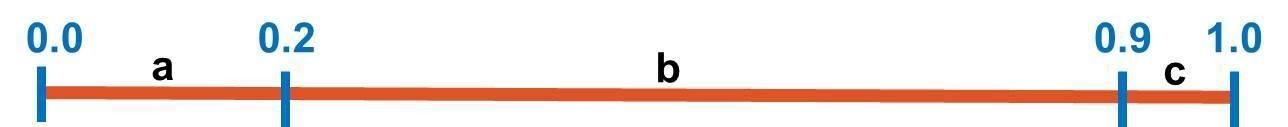
Here are some notes:

The first symbol starts from the same start point of the line (0.0) and the last symbol ends at the endpoint of the line (1.0).
A symbol C covers a percentage of the range that corresponds to its probability. For example, the symbol b covers 70% of the line because its probability is 0.7.

Restricting the interval

AE works by restricting the line interval, which starts from 0.0 to 1.0, through some stages equal to the number of symbols in the message. In this example, there are just 3 symbols in the message, so there are just 3 stages.

In each stage, the line’s interval is restricted according to the sub-interval of the current symbol.

After all symbols are processed, AE returns a single double value encoding the entire message.

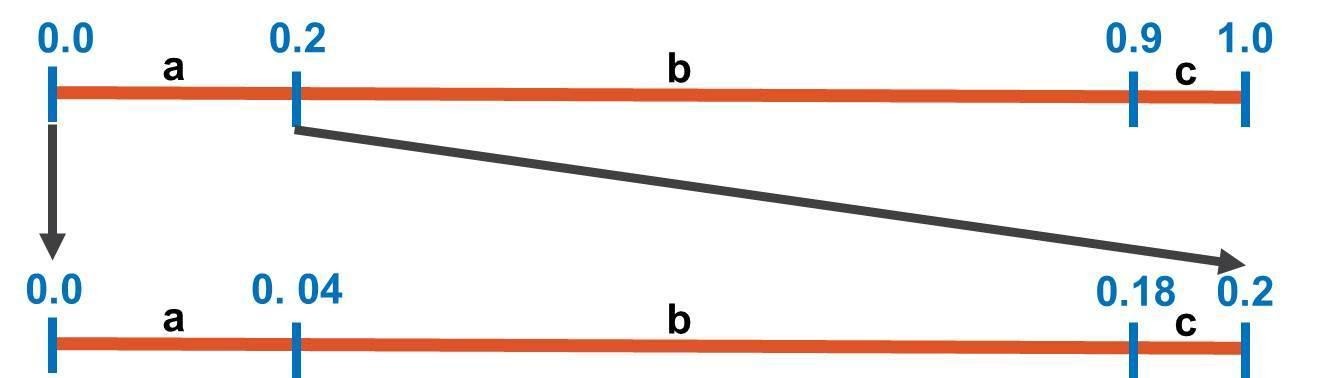
Now, it’s time to look at the message to be encoded, abc, and work on the first symbol a to restrict the line interval.Based on the previous figure, the symbol a covers the interval from 0.0 to 0.2. This interval becomes the line’s interval. In other words, the line interval changes from 0.0:1.0 to 0.0:0.2 as in the next figure. Note that symbol a starts from 0.0 and the last symbol, c, ends at 0.2.

To calculate the interval of each symbol, we’ll use the already mentioned formula:

S+(P(C))*R

Because the line’s range has changed, R changes to 0.2-0.0=0.2. Let’s calculate the start and end values for each symbol:

For the first symbol, a, it starts from 0.0 to 0.0+(0.2)*0.2=0.04. The start value is 0.0 because it’s the first symbol. The range is (0.0:0.04).
For the second symbol b, it starts from 0.04 to 0.04+(0.7)*0.2=0.18. The range is (0.04:0.18).
The third symbol c starts from 0.18 to 0.18+(0.1)*0.2=0.2. The range is (0.18:0.2).

At the end of the first stage, here is the figure that shows the start and end values of each symbol’s interval.

Note that each symbol takes a portion of the line equal to its probability. For example, the probability of the symbol b is 0.7 and thus it takes 70% of the line’s interval.

The next figure summarizes the progress of AE at this point. Let’s start the second stage, which just repeats what we did in the first stage.

The next symbol in the message is b. According to the latest line interval (0.0 to 0.2), the symbol b starts from 0.04 to 0.18. In this stage, the interval of the line will be further restricted to b’s interval, as shown in this figure:

Because the line’s interval changed to (0.04:0.18), R also changes. Its new value is 0.18-0.04=0.14. Let’s calculate the start and end values for each symbol:

For the first symbol, a, it starts from 0.04 to 0.04+(0.2)*0.14=0.068. The range is (0.04:0.068).
For the second symbol, b, it starts from 0.068 to 0.068+(0.7)*0.14=0.166. The range is (0.068:0.166).
The third symbol, c, starts from 0.166 to 0.166+(0.1)*0.14=0.18. The range is (0.166:0.18).

The next figure summarizes the intervals of the 3 symbols. This marks the end of the second stage.

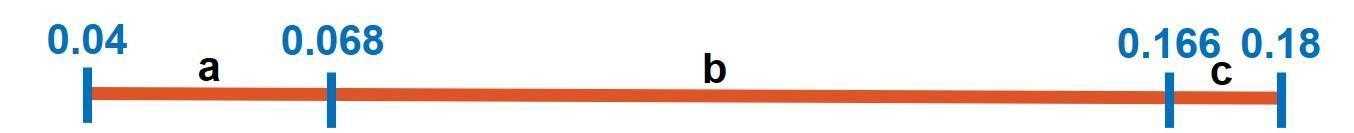
To summarize the progress made up to this point, the next figure connects the 2 completed stages. Let’s move to the third stage.

The third and last symbol in the message is c. According to the latest stage, this symbol falls within the range starting from 0.166 and ending at 0.18. c’s current interval will be the next interval of the line according to the next figure. R for this new line is 0.18-0.166=0.014.

On that line, similarly to previous 2 stages, here are the intervals of the 3 symbols:

symbol a starts from 0.166 to 0.166+(0.2)*0.014=0.1688. The range is (0.166 :0.1688).
symbol b starts from 0.1688 to 0.1688+(0.7)*0.014=0.1786. The range is (0.1688 :0.1786).
symbol c starts from 0.1786 to 0.1786+(0.1)*0.014=0.18. The range is (0.1786:0.18).

The intervals are reflected in the next figure.

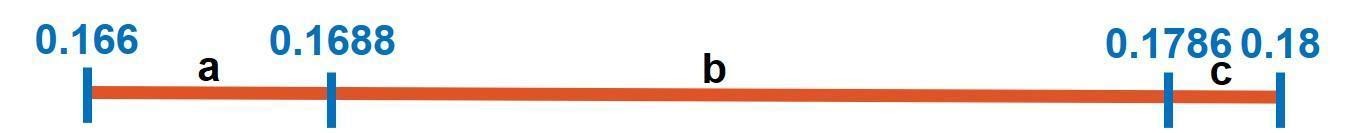
There are no more symbols in the message. The next figure summarizes the calculations from the initial interval (0.0:1.0) to the last interval (0.166:0.18).

Given that AE completed the encoding process, the next subsection calculates the single number that encodes the entire message.

Single value encoding the message

The latest interval reached by AE starts from 0.166 to 0.18. Within this range, any value can be used to encode the entire message. For example, the value could be 0.17.

Through this tutorial, the value is the average of the interval which is:

(0.166+0.18)/2=0.173

So, based on the frequency table used, the message abc is encoded as the value 0.173. When the frequency table changes, then the value that encodes the message changes too.

This marks the end of the encoding process. Now let’s discuss the decoding process.

Decoding

The inputs for decoding are:

The single value that encodes the message.
The frequency table. It should be identical to the one used for encoding.
The number of symbols in the original message.

In our example, the value that encodes the message is 0.173. The frequency table is [a=2, b=7, c=1]. The number of symbols in the message is 3.

The first step of decoding is to calculate the probabilities of the symbols out of their frequency, similarly to what we did before.

The probability table is [p(a)=0.2, p(b)=0.7, p(c)=0.1]. Based on the probability table, the decoding process works similarly to encoding by constructing the same intervals.

First, a line starting from 0.0 and ending at 1.0 is created according to the next figure. The intervals of the 3 symbols are calculated using the same equation used for encoding the message.

S+(P(C))*R

The value 0.173 falls within the first interval (0.0:0.2). Thus, the first symbol in the encoded message is a. As a result, the line’s interval is restricted to the interval that starts from 0.0 to 0.2.

The value 0.173 falls within the second interval (0.04:0.18). Thus, the second symbol in the encoded message is b. In the next figure, the interval will be restricted to the interval 0.04 to 0.18.

The value 0.173 falls within the third interval (0.166:0.18). This is why the next symbol in the message is c.

Remember that the number of symbols in the original message is 3. After decoding 3 symbols, the decoding process is completed. The decoded message is abc.

Let’s look at another example.

Example #2

In this example, I won’t detail the steps like before.

There are 4 symbols available to build messages – a, b, c, and d. The frequencies of these symbols are:

Based on the frequency table, here are the probabilities of the symbols:

p(a)=2/10=0.2
p(b)=3/10=0.3
p(c)=1/10=0.1
p(d)=4/10=0.4

The next figure shows the cumulative probabilities of the symbols where the interval of each symbol is equal to its probability.

Now, it’s time for the message to be encoded, which is bdab.

In the first stage, the first symbol in this message, b, is processed. The interval will be restricted to b‘s interval that starts from 0.2 to 0.5.

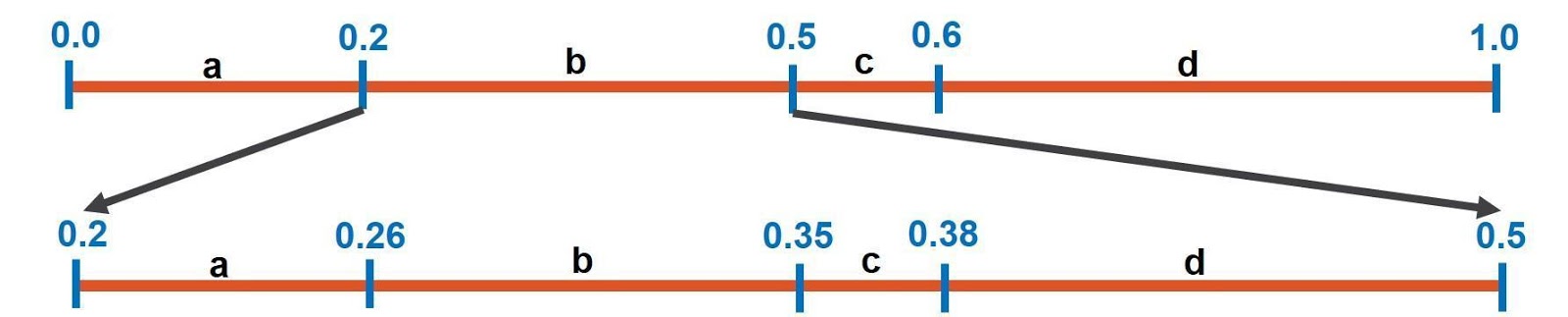
In the second stage, the next symbol in the message is d. As in the next figure, the line’s interval will be restricted to the interval of d which starts from 0.38 to 0.5.

Because the next symbol in the message is a, the interval of the third stage is restricted to start from 0.38 and end at 0.404.

In the fourth and last stage, the next symbol is b, so the interval is restricted to be from 0.3848 to 0.392.

At the end of the last stage, the interval is from 0.3848 to 0.392. To encode the entire message, any value within the interval would be used.

The average value is used in this example, which is 0.3884. This marks the end of the encoding process.

(0.3848+0.392)/2=0.3884

The decoding process starts given the following 3 inputs:

The value that encodes the message, 0.3884.
The frequency table.
The length of the message, 4.

The decoder starts by preparing the probability table similar to what the encoder did. Note that the decoder constructs the same graph in the previous figure.

Here is how the decoding process works:

By checking the initial interval that starts from 0.0 to 1.0, the value 0.3884 falls within the interval of symbol b. Thus, the first symbol in the message is b.
In the next interval that starts from 0.2 to 0.5, the value 0.3884 falls within d‘s interval that starts from 0.38 to 0.5. Thus, the second symbol is d.
The next interval is restricted to d‘s interval where the value 0.3884 falls within the interval of symbol a. Thus, the third symbol is a.
In the next interval, the value 0.3884 falls within the interval of symbol b and thus the fourth and last symbol in the message is b.

After passing through some stages equal to the length of the message, which is 4, the decoded message is bdab.

Up to this point, the theory behind arithmetic encoding is clear. We’re ready to implement this algorithm in Python.

Before starting, we will discuss an important module called decimal, which is essential to implement the AE algorithm successfully.

decimal Module

The AE technique encodes the entire message, regardless of its length, into a single floating-point number.

In Python, the float data type is restricted to a limited number of decimal digits. A Python float cannot accurately save a number beyond this number of decimal digits. The exact number of digits is returned using the dig attribute in the structseq sys.float_info as in the next code (documentation reference).

import sys

print(sys.float_info.dig)

For example, when creating a float variable with the value 123456789.12345678998, the actual stored value is 123456789.12345679, which is different from the original value.

print(float(123456789.12345678998))

In AE, this is a disaster because each digit makes a difference. For AE to work with the float type, the message must be restricted to a few symbols.

In Python, there is a module called decimal that works with a user-defined precision. You can store a number with any amount of decimal digits (documentation reference).

The default precision of decimal values is 28, as returned by the getcontext().prec attribute.

from decimal import getcontext

getcontext().prec # 28

This precision can be changed if the number to be stored exceeds the precision 28. The next line sets the precision to 1500.

getcontext().prec = 1500

According to this page, the maximum precision for 32-bit systems is 425000000. It is 999999999999999999 for 64-bit systems. This is large enough to encode huge messages.

print(decimal.MAX_PREC)

The next subsection creates a decimal value.

Create a decimal value

The decimal module has a class named Decimal which creates decimal values. Below is an example. This way, a number of any precision can be created.

from decimal import Decimal

a = Decimal(1.5)

Note that precision only matters when doing arithmetic operations. Even if the precision of the created decimal value exceeds the precision specified in getcontext().prec, the decimal value will not be restricted to that precision. It will be restricted only when doing arithmetic operations.

In the next code, we create a decimal value that stores a large number. When printing a, the value will be returned without losing any digit.

a = Decimal(‘123456789.12345679104328155517578125’)

When applying an arithmetic operation, like adding 1 to that number, the precision in the getcontext().prec property will take effect to restrict the number of decimal digits. The result of the next code will be 123456790.1234567910432815552, where some digits at the end are clipped.

b = a + 1
print(b) # Decimal(‘123456790.1234567910432815552’)

To fix this issue, you should increase precision.

Change the precision

The decimal module lets you increase the precision by setting a value larger than the default 28 to getcontext().prec. After setting the precision to 40, the result of the next code is 123456790.12345679104328155517578125, where there are no clipped digits.

getcontext().prec = 40

a = Decimal('123456789.12345679104328155517578125')
b = a + 1
print(b) # Decimal('123456790.12345679104328155517578125')

Now let’s build a Python implementation of the arithmetic encoding algorithm.

Python implementation

We build the implementation of AE as a class named ArithmeticEncoding, within a module named pyae.py. The constructor of this class accepts the frequency table, as in the next code.

def __init__(self, frequency_table):
    self.probability_table = self.get_probability_table(frequency_table)

The frequency table passed to this method is a dictionary where each item has a string key representing the symbol, and an integer value representing the frequency. Here’s an example:

{"a": 2,
 "b": 3,
 "c": 1,
 "d": 4}

The constructor calls a method called get_probability_table(). It accepts the frequency table and returns the probability table that’s stored in the probability_table instance attribute.

Here’s the implementation of the get_probability_table method. It simply divides the frequency of each symbol by the sum of all frequencies in the table.

def get_probability_table(self, frequency_table):
    total_frequency = sum(list(frequency_table.values()))

    probability_table = {}
    for key, value in frequency_table.items():
        probability_table[key] = value/total_frequency

    return probability_table

The returned probability table is a dictionary similar to that used for frequencies. Here’s the probability table out of the previous frequency table.

{'a': 0.2,
 'b': 0.3,
 'c': 0.1,
 'd': 0.4}

Encoder

The ArithmeticEncoding class has a method called encode() that encodes the message. It accepts 2 arguments:

msg: The message to be encoded.
probability_table: The probability table.

Here is the implementation of the encode() method. It has a loop with a number of iterations equal to the length of the message.

def encode(self, msg, probability_table):
    encoder = []

    stage_min = Decimal(0.0)
    stage_max = Decimal(1.0)

    for msg_term_idx in range(len(msg)):
        stage_probs = self.process_stage(probability_table, stage_min, stage_max)

        msg_term = msg[msg_term_idx]
        stage_min = stage_probs[msg_term][0]
        stage_max = stage_probs[msg_term][1]

        encoder.append(stage_probs)

    stage_probs = self.process_stage(probability_table, stage_min, stage_max)
    encoder.append(stage_probs)

    encoded_msg = self.get_encoded_value(encoder)

    return encoder, encoded_msg

In each iteration, one symbol of the message is processed in a stage using the process_stage() method. This method simply accepts the probability table and the current interval, and returns a dictionary of the intervals of each symbol within the current stage.

Here is the dictionary returned after the first iteration. This dictionary is appended to a list called encoder, which holds the intervals of all stages.

{
    'a': [Decimal('0.0'), Decimal('0.2')],
    'b': [Decimal('0.2'), Decimal('0.5')],
    'c': [Decimal('0.5'), Decimal('0.6')],
    'd': [Decimal('0.6'), Decimal('1.0')]
}

Based on the next symbol in the message and the result returned by the process_stage method, the new interval is determined.

After processing all the stages, the get_encoded_value() method is called. It returns the value that encodes the entire message. This value is the average of the interval in the last stage.

In this example, the value is 0.3884. The encoder returns this value in addition to the encoder list. When the message is bdab, below is the encoder list. Each item in the list is a dictionary representing a stage. Each dictionary holds the intervals of each symbol.

[
 {'a': [Decimal('0'),
        Decimal('0.2')],
  'b': [Decimal('0.2'),
        Decimal('0.5')],
  'c': [Decimal('0.5'),
        Decimal('0.6')],
  'd': [Decimal('0.6'),
        Decimal('1.0')]},

 {'a': [Decimal('0.2'),
        Decimal('0.26')],
  'b': [Decimal('0.26'),
        Decimal('0.35')],
  'c': [Decimal('0.35'),
        Decimal('0.38')],
  'd': [Decimal('0.38'),
        Decimal('0.5')]},

 {'a': [Decimal('0.38'),
        Decimal('0.404')],
  'b': [Decimal('0.404'),
        Decimal('0.44')],
  'c': [Decimal('0.44'),
        Decimal('0.452')],
  'd': [Decimal('0.452'),
        Decimal('0.5')]},

 {'a': [Decimal('0.38'),
        Decimal('0.3848')],
  'b': [Decimal('0.3848'),
        Decimal('0.392')],
  'c': [Decimal('0.392'),
        Decimal('0.3944')],
  'd': [Decimal('0.3944'),
        Decimal('0.404')]},

 {'a': [Decimal('0.3848'),
        Decimal('0.38624')],
  'b': [Decimal('0.38624'),
        Decimal('0.3884')],
  'c': [Decimal('0.3884'),
        Decimal('0.38912')],
  'd': [Decimal('0.38912'),
        Decimal('0.392')]}
]

Decoder

The decoder is implemented in the ArithmeticEncoding class using the decode() method listed below. It accepts the following 3 arguments:

encoded_msg: The value that encodes the message.
msg_length: The original message length.
probability_table: The probability table used in the encoding process.

It works similarly to the encode() message as it iterates through some iterations equal to the message length.

Through each iteration, the process_stage() method is called to find the intervals of each symbol. These intervals are inspected to find the interval that bounds the value encoding the message.

Once the interval is located, its corresponding symbol is the next in the original message.

def decode(self, encoded_msg, msg_length, probability_table):
    decoder = []
    decoded_msg = ""

    stage_min = Decimal(0.0)
    stage_max = Decimal(1.0)

    for idx in range(msg_length):
        stage_probs = self.process_stage(probability_table, stage_min, stage_max)

        for msg_term, value in stage_probs.items():
            if encoded_msg >= value[0] and encoded_msg <= value[1]:
                break

        decoded_msg = decoded_msg + msg_term
        stage_min = stage_probs[msg_term][0]
        stage_max = stage_probs[msg_term][1]

        decoder.append(stage_probs)

    stage_probs = self.process_stage(probability_table, stage_min, stage_max)
    decoder.append(stage_probs)

    return decoder, decoded_msg

Once a number of symbols equal to the message length are found, the decoding process ends.

Complete code

The complete code of the pyae.py module is listed below. For the most up-to-date code, check this GitHub project.

from decimal import Decimal

class ArithmeticEncoding:
    """
    ArithmeticEncoding is a class for building arithmetic encoding.
    """

    def __init__(self, frequency_table):
        self.probability_table = self.get_probability_table(frequency_table)

    def get_probability_table(self, frequency_table):
        """
        Calculates the probability table out of the frequency table.
        """
        total_frequency = sum(list(frequency_table.values()))

        probability_table = {}
        for key, value in frequency_table.items():
            probability_table[key] = value/total_frequency

        return probability_table

    def get_encoded_value(self, encoder):
        """
        After encoding the entire message, this method returns the single value that represents the entire message.
        """
        last_stage = list(encoder[-1].values())
        last_stage_values = []
        for sublist in last_stage:
            for element in sublist:
                last_stage_values.append(element)

        last_stage_min = min(last_stage_values)
        last_stage_max = max(last_stage_values)

        return (last_stage_min + last_stage_max)/2

    def process_stage(self, probability_table, stage_min, stage_max):
        """
        Processing a stage in the encoding/decoding process.
        """
        stage_probs = {}
        stage_domain = stage_max - stage_min
        for term_idx in range(len(probability_table.items())):
            term = list(probability_table.keys())[term_idx]
            term_prob = Decimal(probability_table[term])
            cum_prob = term_prob * stage_domain + stage_min
            stage_probs[term] = [stage_min, cum_prob]
            stage_min = cum_prob
        return stage_probs

    def encode(self, msg, probability_table):
        """
        Encodes a message.
        """

        encoder = []

        stage_min = Decimal(0.0)
        stage_max = Decimal(1.0)

        for msg_term_idx in range(len(msg)):
            stage_probs = self.process_stage(probability_table, stage_min, stage_max)

            msg_term = msg[msg_term_idx]
            stage_min = stage_probs[msg_term][0]
            stage_max = stage_probs[msg_term][1]

            encoder.append(stage_probs)

        stage_probs = self.process_stage(probability_table, stage_min, stage_max)
        encoder.append(stage_probs)

        encoded_msg = self.get_encoded_value(encoder)

        return encoder, encoded_msg

    def decode(self, encoded_msg, msg_length, probability_table):
        """
        Decodes a message.
        """

        decoder = []
        decoded_msg = ""

        stage_min = Decimal(0.0)
        stage_max = Decimal(1.0)

        for idx in range(msg_length):
            stage_probs = self.process_stage(probability_table, stage_min, stage_max)

            for msg_term, value in stage_probs.items():
                if encoded_msg >= value[0] and encoded_msg <= value[1]:
                    break

            decoded_msg = decoded_msg + msg_term
            stage_min = stage_probs[msg_term][0]
            stage_max = stage_probs[msg_term][1]

            decoder.append(stage_probs)

        stage_probs = self.process_stage(probability_table, stage_min, stage_max)
        decoder.append(stage_probs)

        return decoder, decoded_msg

Example of using the pyae.ArithmeticEncoding class

To use the pyae.ArithmeticEncoding class, follow these steps:

Import pyae
Instantiate the ArithmeticEncoding Class
Prepare a Message
Encode the Message
Decode the Message

Here is the code of an example that encodes the message bdab using the frequency table given in frequency_table variable.

import pyae

frequency_table = {"a": 2,
                   "b": 3,
                   "c": 1,
                   "d": 4}

AE = pyae.ArithmeticEncoding(frequency_table)

original_msg = "bdab"
print("Original Message: {msg}".format(msg=original_msg))

encoder, encoded_msg = AE.encode(msg=original_msg,
                                 probability_table=AE.probability_table)
print("Encoded Message: {msg}".format(msg=encoded_msg))

decoder, decoded_msg = AE.decode(encoded_msg=encoded_msg,
                                 msg_length=len(original_msg),
                                 probability_table=AE.probability_table)
print("Decoded Message: {msg}".format(msg=decoded_msg))

print("Message Decoded Successfully? {result}".format(result=original_msg == decoded_msg))

Here are the messages printed by the code. Because the precision used in the decimal module is enough to encode the message, the message was decoded successfully.

Original Message: bdab
Encoded Message: 0.3884
Decoded Message: bdab
Message Decoded Successfully? True

Applications in Deep Learning

One deep learning AE application of high interest is image and video compression.

It’s used with deep autoencoders to achieve high-quality image compression with very small bits per pixel (bpp).

One of the recent papers that use AE is: Cheng, Zhengxue, et al. “Learning image and video compression through spatial-temporal energy compaction.” Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019.

The next figure is taken from the paper that summarizes how things work.

The Analysis Transform block represents the encoder of the autoencoder. Its latent vector is fed to a quantization step. The output of the quantization is encoded using arithmetic encoding. The value that encodes the quantized vector is converted into binary.

The binary string is then decoded using the arithmetic encoding to be fed to the Synthesis Transform block which represents the decoder of the autoencoder.

Conclusion

This concludes my introduction to the arithmetic encoding algorithm. AE encodes the entire message into a single floating-point number.

We went over the detailed steps of AE based on 2 examples, within which it is clear how the encoder and the decoder work.

We also built a Python implementation of this algorithm which is available on GitHub.

The implementation has just a single module named pyae.py, which has a class named ArithmeticEncoding that builds the algorithm.

One cool application of arithmetic encoding in deep learning is compressing images with high quality while achieving a very low bits per pixel (bpp) rate.

In later tutorials, I’ll provide more details about arithmetic encoding, like an in-depth discussion of the applications of arithmetic encoding. The implementation will be extended to work with various types of data. Also, the decimal value returned from the encoding process will be converted into binary.

For now, thanks for reading!